En veldig viktig og mye brukt komponent i elektronikken er kondensatoren.
Kondensatoren virker som et lager for energi, vi kan sammenligne den med et lite batteri, som kan lades opp og lades ut veldig raskt.
I skjema og regnestykker angis kondensatorer som C, og størrelsen kalles kapasitans. Kapasitansen måles i Farad, F.
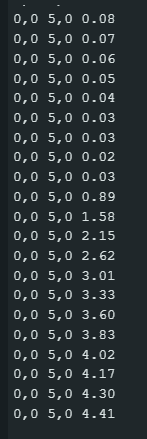
Figuren under viser et par vanlige symboler for kondensatorer. Den ene er en upolarisert kondensator, dvs. at det ikke har noe si hvilken vei de kobles. Dette er som oftest verdier fra noen få pF (picoFarad) og opp til noen hundre nF (nanoFarad). Når verdiene kommer opp i μF (mikroFarad) er kondensatorene som oftest polariserte, som på symbolet til høyre. Disse er merket enten med + eller -, slik at de ikke blir koblet med feil polaritet. Feilkobling kan føre til ødelagt kondensator, eller i verste fall en liten eksplosjon.
(Det finnes unntak på dette med størrelsene, f.eks. start- eller driftskondensatorer for motorer, som kan være noen μF)
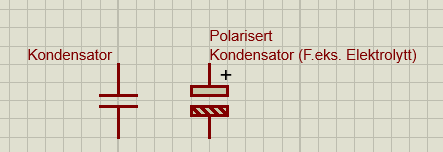
Her skal vi se på spenningskurver over kondensatoren når den lades opp, og når den lades ut. Koblingen er veldig enkel, bare kondensatoren og en resistor (motstand) for å begrense strømmen.
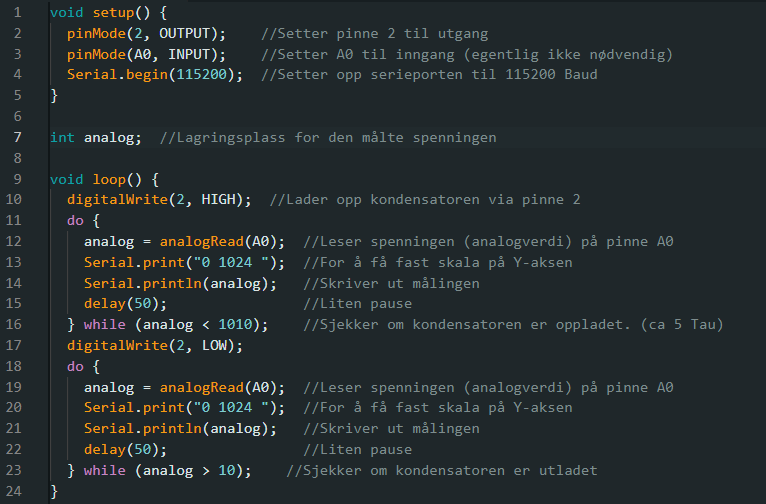
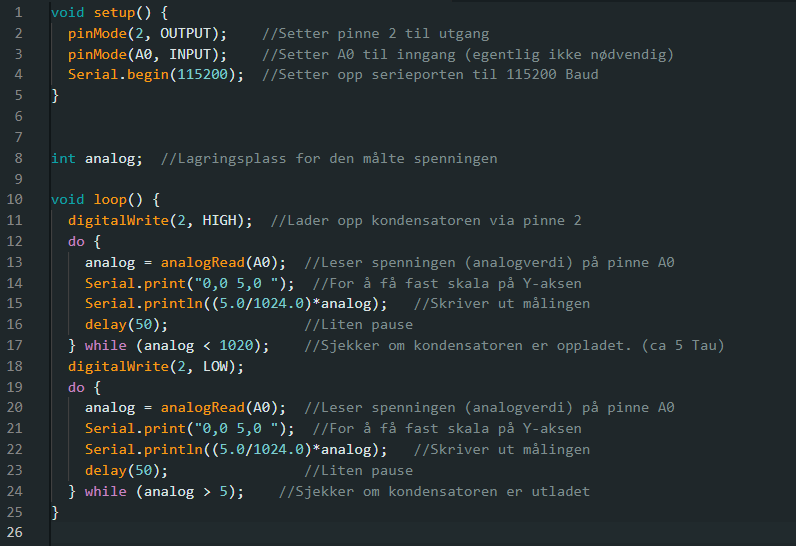
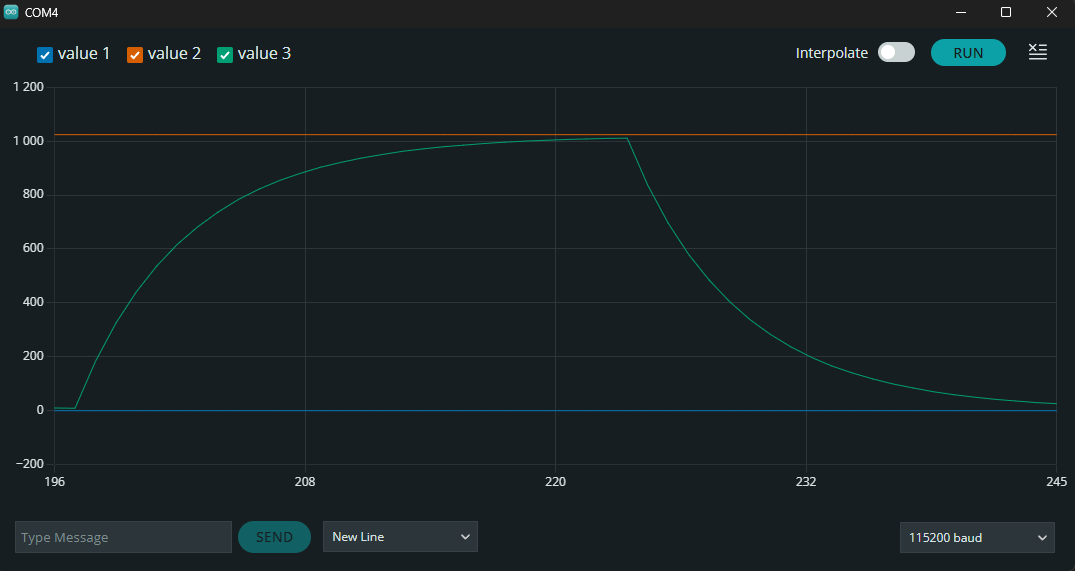
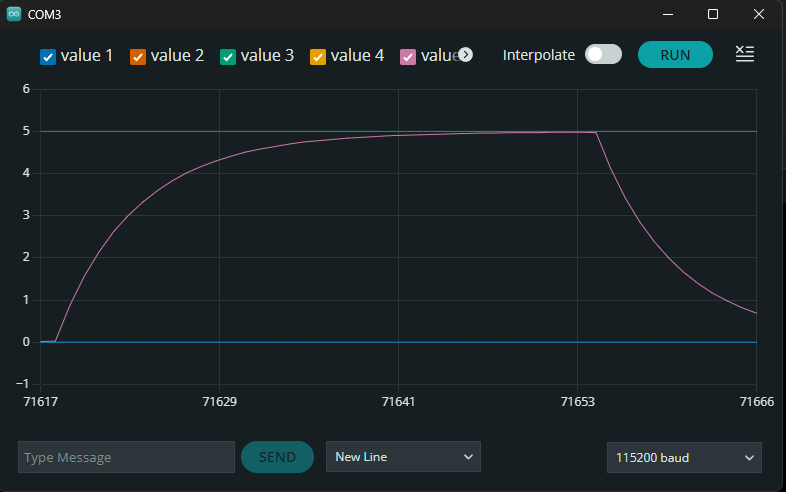
Oppgave 1: Koble opp etter skjemaet under "Oppkobling". Skriv et program som lader opp kondensatoren med strøm fra pinne 2. Mens kondensatoren lades opp, skal du ta analoge målinger med pinne A0, og skrive målingene til serieporten. Når kondensatoren er (tilnærmet) fullt oppladet, skal den lades ut igjen gjennom samme pinne. Mål på samme måte som med oppladingen. Når kondensatoren er oppladet, starter hele prosessen på nytt. Se resultatene på Serial Plotter. Oppgave 2: Skriv om koden slik at du viser den målte spenningen, i stedet for verdien direkte fra ADC'en. Dette er et forslag til løsning. Hvis du endrer verdier på motstand eller kondensator må du kanskje endre delay'ene. Oppgave 1: Oppgave 2:Oppkobling
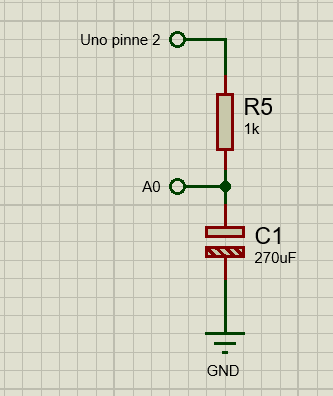
En veldig enkel kobling til dette eksperimentet. Her går det an å eksperimenter med verdier. Hvis du bruker en mindre kondensator, bør du gå opp i verdi på resistoren. Tidskonstanten τ (Tau) er R*C, og den bør havne på ca. det samme for at vi skal rekke å ta noen målinger for hver opp- og utlading.
Oppgave
Løsningsforslag